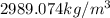Question

A wood salvage company is hoisting an old tree trunk off the bottom and out of a lake. The cable from the hoist is tied around the log above its center of mass. The hoist applies a force of 9,800 N to the cable to suspend the log in the lake water (FT water), and a force of 29,000 N to suspend the log above the lake surface (FT air). What are the volume and density of the log? Assume the lake water has a density of 1,007 kg/m3.

Answer 1

To solve this problem it is necessary to resort to the concepts expressed in the Buoyancy Force.

The buoyancy force is given by the equation

`F = \rho Vg`

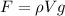
Where,

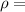`\rho =` Density

V =Volume

g = Gravitational Acceleration

PART A) From the given data we can find the volume, so

`9800 = 1007*V*9.8`

`V = 0.99m^3`

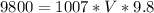
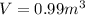
PART B) The mass can be expressed from the Newton equation in which

`F = mg`

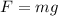
Where,

m = mass

g = Gravitational acceleration

Replacing with our values we have that

`29000 = m*9.8`

`m = 2959.18Kg`

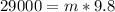
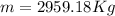
Therefore the Density can be calculated with the ratio between the Volume and Mass

`\rho = (m)/(V)`

`\rho = (2959.18Kg)/(0.99m^3)`

`\rho = 2989.074kg/m^3`

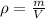
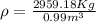
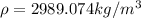
Therefore the Density of the log is
`2989.074kg/m^3`