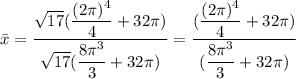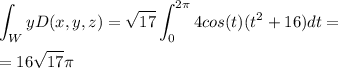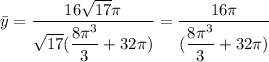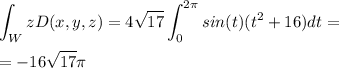Answer:
Mass
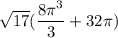
Center of mass
Coordinate x
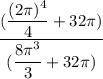
Coordinate y
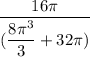
Coordinate z
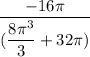
Explanation:
Let W be the wire. We can consider W=(x(t),y(t),z(t)) as a path given by the parametric functions
x(t) = t
y(t) = 4 cos(t)
z(t) = 4 sin(t)
for 0 ≤ t ≤ 2π
If D(x,y,z) is the density of W at a given point (x,y,z), the mass m would be the curve integral along the path W
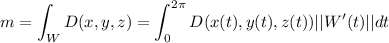
The density D(x,y,z) is given by
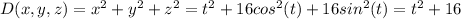
on the other hand
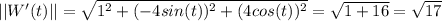
and we have
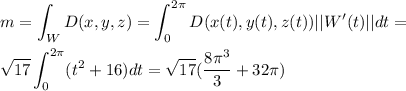
The center of mass is the point
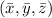
where
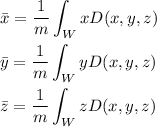
We have
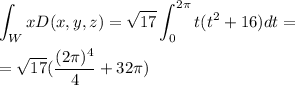
so