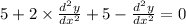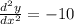Question

Please help on implicit differentiation problem.

Answer 1

`( d^(2) y)/(dx^(2) ) = -10`

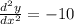
Explanation:

Concept : We have to differentiate the given equation twice and then put the values of x and y at the given point.

The given point is (2,-5).

Given xy - y = -5

Differentiating both sides,

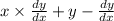`x * (dy)/(dx) + y - (dy)/(dx)` = 0

Substitute (x,y) as (2,-5)

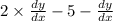`2 * (dy)/(dx) -5 - (dy)/(dx)` = 0

`(dy)/(dx) = 5`

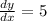
Differentiating again, we get

`(dy)/(dx) + x * ( d^(2) y)/(dx^(2) ) + (dy)/(dx) - ( d^(2) y)/(dx^(2) ) = 0`

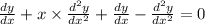
Substitute values of x , y and \frac{dy}{dx} ,

`5 + 2 * ( d^(2) y)/(dx^(2) ) + 5 - ( d^(2) y)/(dx^(2) ) = 0`

`( d^(2) y)/(dx^(2) ) = -10`