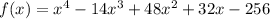Question

Find a polynomial of degree 4 and the zeros are -2, 4, 4, 8

Answer 1

Required polynomial of degree four having zeros as -2 , 4 , 4 , 8 is
`f(x)=x^(4)-14 x^(3)+48 x^(2)+32 x-256`

Solution:

Need to determine a polynomial of degree 4 and the zeros are -2, 4 , 4 and 8

Let the required polynomial be represented by f(x)

The factor theorem describes the relationship between the root of a polynomial and a factor of the polynomial.

If the polynomial p(x) is divided by cx−d and the remainder, given by p(d/c), is equal to zero, then cx−d is a factor of p(x).

-2 is zero of a polynomial means when x = -2, f(-2) = 0, so from factor theorem we can say that

=> x = -2 that is x + 2 = 0 is factor of polynomial f(x)

4 is zero of a polynomial means when x = 4, f(4) = 0 , so from factor theorem we can say that

=> x = 4 that is x -4 = 0 is factor of polynomial f(x)

4 is zero of a polynomial means when x = 4, f(4) = 0 , so from factor theorem we can say that

=> x = 4 that is x -4 = 0 is factor of polynomial f(x)

8 is zero of a polynomial means when x = 8, f(8) = 0 , so from factor theorem we can say that

=> x = 8 that is x -8 = 0 is factor of polynomial f(x)

So now we have four factors of polynomial f(x) that are (x + 2), (x -4) , (x -4) and (x – 8)

And as given that degree of polynomial f(x) is 4

Now f(x) is equal to product of factors

`\begin{array}{l}{\Rightarrow f(x)=(x+2)(x-4)^(2)(x-8)} \\\\ {=>f(x)=(x+2)\left(x^(2)-8 x+16\right)(x-8)} \\\\ {=>f(x)=(x+2)\left(x^(3)-8 x^(2)+16 x-8 x^(2)+64 x-128\right)} \\\\ {=>f(x)=(x+2)\left(x^(3)-16 x^(2)+80 x-128\right)} \\\\ {=>f(x)=x\left(x^(3)-16 x^(2)+80 x-128\right)+2\left(x^(3)-16 x^(2)+80 x-128\right)} \\\\ {=>f(x)=x^(4)-16 x^(3)+80 x^(2)-128 x+2 x^(3)-32 x^(2)+160 x-256} \\\\ {=>f(x)=x^(4)-14 x^(3)+48 x^(2)+32 x-256}\end{array}`

Hence required polynomial of degree four having zeros as -2 , 4 , 4 , 8 is
`f(x)=x^(4)-14 x^(3)+48 x^(2)+32 x-256`