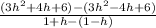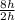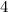Question

If y=3x^2 - 2x +5

What is the average slope for this function between the points at:


i. x= -3 and x= -1


ii. x=-3 and x=0


iii. x= 1-h and x= 1+h


USE DIFFERENCE QUOTIENT FORMULA.

Answer 1

Part i) -14

Part ii) 11

Part iii) 4

Explanation:

we know that

The average rate of change or slope using the difference quotient formula is equal to

`(f(b)-f(a))/(b-a)`

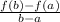
Part i) x= -3 and x= -1

In this problem we have

`a=--3`

`b=-1`

`f(a)=f(-3)=3(-3)^(2) -2(-3)+5=38`

`f(b)=f(-1)=3(-1)^(2) -2(-1)+5=10`

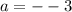
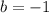
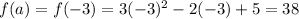
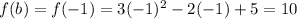
Substitute

`(10-38)/(-1+3)`

`(-28)/(2)`

`-14`

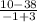
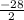
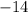
Part ii) x= -3 and x= 0

In this problem we have

`a=--3`

`b=0`

`f(a)=f(-3)=3(-3)^(2) -2(-3)+5=38`

`f(b)=f(0)=3(0)^(2) -2(0)+5=5`

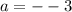
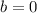
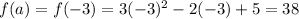
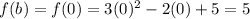
Substitute

`(5-38)/(0+3)`

`(-33)/(3)`

`-11`

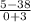
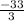
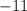
Part iii) x= (1-h) and x=(1+h)

In this problem we have

`a=-(1-h)`

`b=(1+h)`

`f(a)=f(1-h)=3(1-h)^(2) -2(1-h)+5=3(1-2h+h^2)-2+2h+5=3-6h+3h^2+2h+3=3h^2-4h+6`

`f(b)=f(1+h)=3(1+h)^(2) -2(1+h)+5=3(1+2h+h^2)-2-2h+5=3+6h+3h^2-2h+3=3h^2+4h+6`

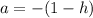
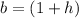
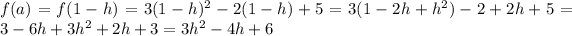
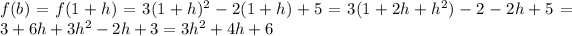
Substitute

`((3h^2+4h+6)-(3h^2-4h+6))/(1+h-(1-h))`

`(8h)/(2h)`

`4`