Answer:
a)
1.35 kg
b)
2.67 ms⁻¹
Step-by-step explanation:
a)
 = mass of first body = 2.7 kg
= mass of first body = 2.7 kg
 = mass of second body = ?
= mass of second body = ?
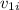 = initial velocity of the first body before collision =
= initial velocity of the first body before collision =

 = initial velocity of the second body before collision = 0 m/s
= initial velocity of the second body before collision = 0 m/s
 = final velocity of the first body after collision =
= final velocity of the first body after collision =
using conservation of momentum equation
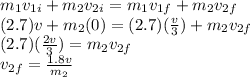
Using conservation of kinetic energy
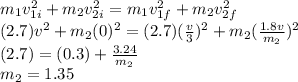
b)
 = mass of first body = 2.7 kg
= mass of first body = 2.7 kg
 = mass of second body = 1.35 kg
= mass of second body = 1.35 kg
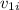 = initial velocity of the first body before collision = 4 ms⁻¹
= initial velocity of the first body before collision = 4 ms⁻¹
 = initial velocity of the second body before collision = 0 m/s
= initial velocity of the second body before collision = 0 m/s
Speed of the center of mass of two-body system is given as
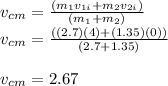 ms⁻¹
ms⁻¹