Question

A spacecraft is placed in a circular orbit around a planet with mass 6.4 x 1023 kg. The spacecraft orbits at a height of 4.5 x 107 m above the planet’s surface. What additional information is needed to calculate the speed of the spacecraft in the orbit?

Answer 1

It is necessary to know the radius of the planet.

Step-by-step explanation:

The speed of the spacecraft can be found by means of the equation of the Universal law of gravity:

`F = G (M.m)/(r^(2))` (1)

Where F is the gravitational force, G is gravitational constant, M is the mass of the planet, m is the mass of the spacecraft and r is the orbital radius of the spacecraft.

Equation 1 can be express in terms of the speed by using Newton's second law and the equation for centripetal acceleration:

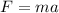`F = ma` (2)

Replacing equation 2 in equation 1 it is gotten:

`ma = G (M.m)/(r^(2))` (3)

the centripetal acceleration is defined as:

`a = (v^(2))/(r)` (4)

Replacing equation 4 in equation 3 it is gotten:

`m(v^(2))/(r) = G (M.m)/(r^(2))` (5)

Then, v can be isolated from equation 5:

`mv^(2) = G (M.m)/(r)`

`v^(2) = G (M.m)/(rm)`

`v^(2) = G (M)/(r)`

`v = \sqrt{(GM)/(r)}`

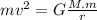
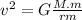
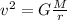
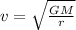
However, the orbital radius of the spacecraft is obtained by the sum of the radius of the planet and the height of the spacecraft above the surface of the planet (r = R+h)

`v = \sqrt{(GM)/(R+h)}` (6)

Hence, by equation 6 it can be concluded that it is necessary to know the radius of the planet in order to calculate the speed of the spacecraft.