Answer:
13,57,31
Explanation:
Given that X, Y , Z be three random variables which satisfy the following conditions:
Var(X) = 4, Var(Y ) = 9, Var(Z) = 16. Cov(X, Y ) = −2, Cov(Z, X) = 3,
Var(y,z) =0 since given as independent
To find
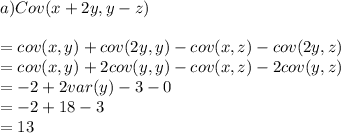
b)
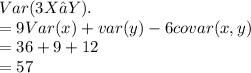
c) Var(X + Y + Z)
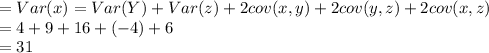
Note:
Var(x+y) = var(x) + Var(Y) +2cov (x,y)
Var(x+2y) = Var(x) +4Var(y)+4cov (x,y)