Question

Case 1: A Styrofoam cup holds an unknown amount of lemonade (which is essentially water) at 20.5 °C. A 0.0550-kg ice cube at -10.2°C is placed in the lemonade. When thermal equilibrium is reached, all the ice has melted and the final temperature of the mixture is measured to be 11.8 °C. Assume that the mass of the cup is so small that it absorbs a negligible amount of heat, and ignore any heat lost to the surroundings. The latent heat of fusion for water is 3.4 X10 J/kg. The specific heat capacity for water and lemonade is the same, 4186 J/(kg °C). The specific heat capacity for ice is 2000 J/(kg °C). The cold ICE absorbs heat in 3 steps: Step 1: COLD ICE warms up from -10.2 °C. to 0.0 °C. (Remember: cold ice DOESN't Melt before reaching 0.0 °C.) Apply Q = mcAT, to the cold ice. Calculate the heat absorbed by the ICE in this step. Keep 2 decimal places. Report all heat as POSITIVE. Enter a number Submit (5 attempts remaining) Step 2: ICE at 0.0 °C melts into water at 0.0 °C. Calculate the heat absorbed by the ICE in this step. Keep 2 decimal places. Report all heat as POSITIVE. Enter a number Submit (5 attempts remaining) Step 3: The water at 0.0 °C from melted ice warms up to 11.8 °C. Apply Q = mcAT, to the water. Calculate the heat absorbed by water in this step. Keep 2 decimal places. Report all heat as POSITIVE. Enter a number Submit (5 attempts remaining) Calculate the total heat absorbed by ICE in the above 3 steps. Enter a number J Submit (5 attempts remaining) The warm lemonade releases heat in cooling down from 20.5 °C to 11.8 °C. Apply Q = mcAT, to the lemonade. Keep mass m as "space hoder. Keep all heat as POSITIVE. Let Q released by lemonade = Total heat absorbed by ICE Find the mass of the lemonade. Keep 2 decimal places. Enter a number kg Submit (5 attempts remaining)

Answer 1

`m_l=0.619\ kg`

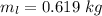
Step-by-step explanation:

Given:

• initial temperature of water(lemonade),
  `T_(il)=20.5^(\circ)C`

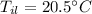
• mass of ice,
  `m=0.055\ kg`

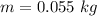
• initial temperature of ice,
  `T_(ii)=-10.2^(\circ)C`

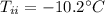
• final temperature of the mixture,
  `T_f=11.8^(\circ)C`

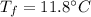
• specific heat capacity of ice,
  `c_i=2000\ J.kg^(-1). ^(\circ)C^(-1)`

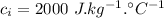
• specific heat capacity of water,
  `c_w=4186\ J.kg^(-1). ^(\circ)C^(-1)`

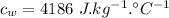
• Latent heat of fusion of ice,
  `L=340000\ J.kg^(-1)`

For the whole ice to melt in lemonade and result a temperature of 11.8°C the total heat lost by the lemonade will be equal to the total heat absorbed by the ice to come to 0°C from -10.2°C along with the latent heat absorbed in the melting of ice at 0°C and the heat absorbed by the ice water of 0°C to reach a temperature of 11.8°C.

Now, mathematically:

`Q_l=Q_i+Q_m+Q_w`

`m_l.c_w.\Delta T_l=m_i.c_i.\Delta T_i_i+m_i.L+m_i.c_w.\Delta T_w`

`m_l.c_w.(T_(il)-T_f)=m_i(c_i.\Delta T_i_i+L+c_w.\Delta T_w)`

`m_l* 4186* (20.5-11.8)=0.055(2000* (0-(-10.2))+340000+4186* (11.8-0))`

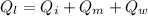
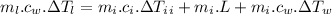
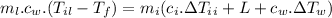
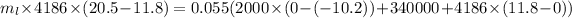
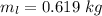`m_l=0.619\ kg` (mass of lemonade)