Question

Find the length of the following curve. If you have a grapher, you may want to graph the curve to see what it looks like. y = (2/3) (x^2 + 1) ^ (3/2) from x = 0 to x = 6 The length of the curve is ___. (Type an exact answer, using radicals as needed.)

Answer 1

Length of curve=150 units

Explanation:

We are given that a curve

`y=(2)/(3)(x^2+1)^{(3)/(2)}`

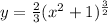
x=0 to x=6

We have to find the length of curve.

Differentiate w.r.t x then we get

`(dy)/(dx)=(2)/(3)* (3)/(2)* (x^2+1)^{(1)/(2)}* 2x=2x(x^2+1)^{(1)/(2)}`

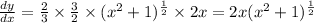
Using formula:
`(dx^n)/(dx)=nx^(n-1)`

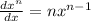
Length of curve=
`\int_(a)^(b)\sqrt{1+((dy)/(dx))^2}dx`

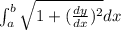
Substitute the value

Then, we get

Length of curve=
`\int_(0)^(6)\sqrt{1+(2x(x^2+1)^{(1)/(2)})^2}dx`

Length of curve=
`\int_(0)^(6)√(1+4x^2(x^2+1))dx`

Length of curve=
`\int_(0)^(6)√(1+4x^4+4x^2)dx=\int_(0)^(6)\sqrt{(2x^2+1)^2dx`

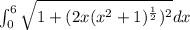
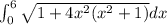
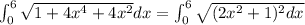
Length of curve=
`\int_(0)^(6)(2x^2+1)dx=[(2x^3)/(3)+x]^(6)_(0)`

Using formula:
`\int_(a)^(b)f(x)dx=f(b)-f(a)`

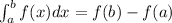
Length of curve=
`(2)/(3)(6)^3+6-0-0=150` units