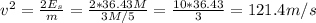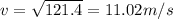Question

A father racing his son has half the kinetic energy of the son, whohas three-fifths the mass of the father. The father speeds up by2.5 m/s and then has the same kinetic energy as the son.a) What is the original speed of the father?b) What is the original speed of the son?

Answer 1

a) 6.04 m/s

b) 11.02 m/s

Step-by-step explanation:

a) Let the father mass be M, and his speed be V. His son mass is m = 3M/5. Since his kinetic energy initially is half of after he increases his speed by 2.5m/s

`E_2 = 2E_1`

`(M(V+2.5)^2)/(2) = 2(MV^2)/(2)`

`V^2 + 5V + 6.25 = 2V^2`

`V^2 - 5V - 6.25 = 0`

`V \approx 6.04m/s`

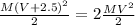
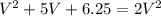
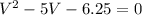
b) The son kinetic energy initially is:

`E_s = 2E_1 = 2(MV^2)/(2) = MV^2 = M*6.04^2 = 36.43M J`

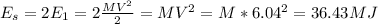
We can solve for the son speed by the following formula

`E_s = (mv^2)/(2)`

`v^2 = (2E_s)/(m) = (2*36.43M)/(3M/5) = (10*36.43)/(3) = 121.4m/s`

`v = √(121.4) = 11.02 m/s`