Question

The length of time a person takes to decide which shoes to purchase is normally distributed with a mean of 8.54 minutes and a standard deviation of 1.91. Find the probability that a randomly selected individual will take less than 6 minutes to select a shoe purchase. Is this outcome unusual?

Answer 1

Answer: 0.0918, it is not unusual.

Explanation:

Given : The length of time a person takes to decide which shoes to purchase is normally distributed with a mean of 8.54 minutes and a standard deviation of 1.91.

i.e.
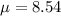`\mu=8.54` minutes and
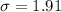`\sigma= 1.91` minutes

Let x denotes the length of time a person takes to decide which shoes to purchase.

Formula :
`z=(x-\mu)/(\sigma)`

Then, the probability that a randomly selected individual will take less than 6 minutes to select a shoe purchase will be :-

`\text{P-value=}P(x<6)=P((x-\mu)/(\sigma)<(6-8.54)/(1.91))\\\\\approx P(z<1.33)=1-P(z<1.33)\ \ \ [\becaus\ P(Z<-z)=1-P(Z<z)]\\\\=1-0.9082\ \ [\text{By using z-value}]=0.0918`

Thus , the required probability = 0.0918

Since, P-value (0.0918) >0.05 , it means this outcome is not unusual.

[Note : When a outcome is unusual then the probability of its happening is less than or equal to 0.05. ]