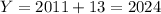Question

During 2012, global oil consumption grew by 0.7%, to reach 88 million barrels per day. Assume that it continues to increase at this rate, (a) Write the first four terms of the sequence a_n giving daily oil consumption n years after 2011; give a formula for the general term a_n. Round your answers for a_1, a_2, a_3, and a_4 to three decimal places.

a_1 =_____________.
a_2 = _____________.
a-3 = _____________.
a_4 = _____________.
a_n = _____________.
(b) In what year is consumption first expected to exceed 195 million barrels a day? Consumption exceeds 195 million barrels per day during the year

Answer 1

(a)

`a_(1) = 88.000 \ million\\a_(2) = 94.160 \ million\\a_(3) = 100.751 \ million\\a_(4) = 107.804 \ million\\a_(n) = 82.243*1.07^n\\`

(b) 2024

Explanation:

Global oil consumption in 2011 is given by:

`C_(2011) =(88)/(1.07)=82.243 \ million`

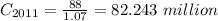
(a) Assuming a constant growth of 0.7% per year, the formula for the daily oil consumption n years after 2011 is:

`a_(n) = a_(0)*1.07^n\\a_(0) = C_(2011) = 82.243\\a_(n) = 82.243*1.07^n`

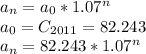
The terms a_1, a_2,a_3 and a_4, corresponding to the global oil consumption in the years of 2012, 2013, 2014 and 2015, respectively, are given by:

`a_(1) = 82.243*1.07^1\\a_(1) = 88.000 \ million\\a_(2) = 82.243*1.07^2\\a_(2) = 94.160 \ million\\a_(3) = 82.243*1.07^3\\a_(3) = 100.751 \ million\\a_(4) = 82.243*1.07^4\\a_(4) = 107.804 \ million\\`

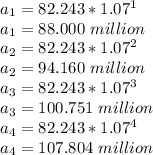
(b) To find the in year in which consumption reaches 195 million barrels a day, apply logarithmic properties:

`a_(n) = 82.243*1.07^n\\ln(a_(n)) = ln(82.243)+ n*ln(1.07)\\\\n=(ln(195)-ln(82.243))/(ln(1.07)) \\n= 12.760`

Consumption will reach 195 million barrels, 12.7 years after 2011, round it to the next whole year to find when consumption exceeds 195 million:

`Y = 2011+13 = 2024`