Answers:
a) 13 s
b) 0.362 m/s
Step-by-step explanation:
We have the following data:
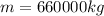 is the mass of the mass damper
is the mass of the mass damper
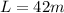 is the length of the pendulum
is the length of the pendulum
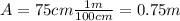 is the amplitude
is the amplitude
a) Period of oscillation:
This can be solved by the following equation:
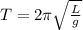 (1)
(1)
Where:
 is the period
is the period
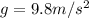 is the acceleration due gravity
is the acceleration due gravity
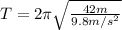 (2)
(2)
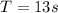 (3)
(3)
b) Maximum Velocity:
The velocity in a pendulum is maximum
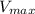 when the pendulum is in its mean position and the amplitude is maximum. So, the equation in this case is:
when the pendulum is in its mean position and the amplitude is maximum. So, the equation in this case is:
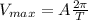 (4)
(4)
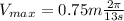 (5)
(5)
