Question

A very long string (linear density 0.7 kg/m ) is stretched with a tension of 70 N . One end of the string oscillates up and down with an amplitude of 7 cm and a period of 0.35 s . What is the wavelength of the waves created in the string?

Answer 1

To develop this problem it is necessary to apply the concepts related to Wavelength, The relationship between speed, voltage and linear density as well as frequency. By definition the speed as a function of the tension and the linear density is given by

`V = \sqrt{(T)/(\rho)}`

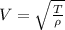
Where,

T = Tension

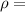`\rho =` Linear density

Our data are given by

Tension , T = 70 N

Linear density ,
`\rho = 0.7 kg/m`

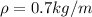
Amplitude , A = 7 cm = 0.07 m

Period , t = 0.35 s

Replacing our values,

`V = \sqrt{(T)/(\rho)}`

`V = \sqrt{(70)/(0.7)`

`V = 10m/s`

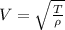
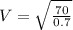
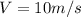
Speed can also be expressed as

`V = \lambda f`

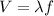
Re-arrange to find \lambda

`\lambda = (V)/(f)`

Where,

f = Frequency,

Which is also described in function of the Period as,

`f = (1)/(T)`

`f = (1)/(0.35)`

`f = 2.86 Hz`

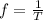
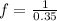
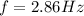
Therefore replacing to find
`\lambda`

`\lambda = (10)/(2.86)`

`\lambda = 3.49m`

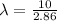
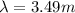
Therefore the wavelength of the waves created in the string is 3.49m