Question

13. In the triangle below, the sides have length x + 3, 3x - 1. and 4x. Determine the range of possible

values of x.

Answer 1

Hence as long as x > 2/3, we can form a triangle from the three given sides.

Explanation:

Given:

Length of 3 sides of triangle are
`x+3, 4x,3x-1`

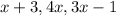
Solution:

From the length of the 2nd side 4x, we know that x > 0

Let this be 1 st statement.

Now from the triangle inequality we can say that;

`x + 3 + 4x > 3x -1\\5x+3>3x-1\\5x-3x>-1-3\\2x>-2\\x>-1`

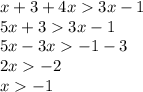
No new information from this because of the 1st statement above.

Also,

`4x + 3x - 1 > x +3\\7x-1>x+3\\7x-x>3+1\\6x>4\\x>(4)/(6)\\\\x>(2)/(3)`

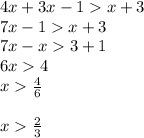
Lastly,

`x+3 +3x - 1 > 4x\\4x-2>4x\\4x-4x>2\\0>2`

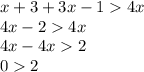
and again no new information is obtained from this inequality.

Hence as long as x > 2/3, we can form a triangle from the three given sides.