Question

In ascending powers of x, find the first 3 terms of the following binomial expression. Then, find a and b.

Answer 1

`\left( 3- \frac x 5 \right)^8`

`= {8 \choose 0} 3^8 (-\frac x 5)^0 + {8 \choose 1} 3^7 (-\frac x 5)^1 + {8 \choose 2} 3^6 (-\frac x 5)^2 + ...`

`=3^8 - 8 3^7 (\frac x 5) + (8(7)/(2(25))) 3^6 x^2+ ...`

`\left( 3- \frac x 5 \right)^8 =6561 - (17496/5)x +(20412/25) x^2 + ...`

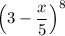
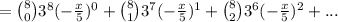
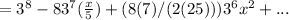
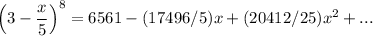
Answer: 6561, -(17496/5) x, (20412/25) x²

The constant term of

`(ax+b)\left( 3- \frac x 5 \right)^8 = (ax+b)(6561 - (17496/5)x +(20412/25) x^2 + ...)`

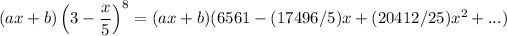
is 6561b so

6165b = 32805

b = 32805/6165 = 729/137

The linear term is

(6561a + (17496/5)b) x

6561a + (17496/5)(729/137) = -4374

a = -7202/2055

Answer: a = -7202/2055, b = 729/137

I expected nicer numbers; I may have made an arithmetic mistake.