Question

Find the explicit formula for the general nth term of the geometric sequence described below.

a4= -32 and a7= -256

an=?

Answer 1

An=-4(2)^n-1

Explanation:

Answer 2

`a_n=-4(2)^(n-1)`

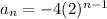
Explanation:

Let the geometric sequence be:

First term:
`a_1=a`

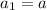
Second term:
`a_2=ar`

Third term:
`a_3=ar^2`

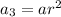
Fourth term:
`a^4=ar^3`

Follow the pattern for the terms between the 4th and 7th: ..........

Seventh term:
`a_7=ar^6`

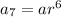
Follow the pattern for the terms between the 7th and the nth: .........

`a_n=ar^(n-1)`

So we need to find
`a` which the value of the first term.

We need to find
`r` which is the common ratio here.

So if we take the 7th term and divide the 4th term we get the following equation:

`(a_7)/(a^4)=(-256)/(-32)`

`(ar^6)/(ar^3)=(-256)/(-32)`

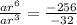
Now the first thing I notice is on the left hand side. I can cancel out some common factors over the numerator and denominator:

`r^(6-3)=8`

`r^(3)=8`

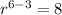
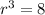
Now I see to find the common ratio,
`r`, we can just take the cube root of both sides:

`r=\sqrt[3]{8}`

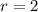`r=2` is true since 2(2)(2)=8.

So after finding
`r` has value 2, we need to find
`a` which is the first term of the sequence.

Let's use one of our equations with a given value for it:

`a_4=-32`

`ar^3=-32`

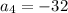
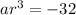
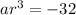`ar^3=-32` with
`r=2`:

`a(2)^3=-32`

`a(8)=-32`

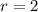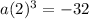
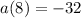
Divide both sides by 8:

`a=(-32)/(8)`

`a=-4`

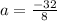
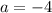
So the first term,
`a`, has value -4.

So the explicit form of this geometric sequence is:

`a_n=-4(2)^(n-1)`

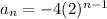
Let's verify:

What happens when
`n=4`?

`a_4=-4(2)^(4-1)`

`a_4=-4(2)^3`

`a_4=-4(8)`

`a_4=-32`

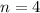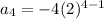
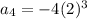
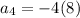
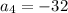
That look's good.

Let's check the other given condition.

`n=7`?

`a_7=-4(2)^(7-1)`

`a_7=-4(2)^(6)`

`a_7=-4(64)`

`a_7=-256`

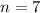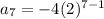
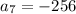
Since both of the conditions are satisfied, we have done our job and it is confirmed.