Question

A study found that the average stopping distance of a school bus traveling 50 mph was 264 feet. a group of automotive engineers decided to conduct a study of its school buses and found that for 40 buses, the average stopping distance of buses traveling 50 mph was 262.3 feet. the standard deviation of the population was 3.0 feet. test the claim that the average stopping distance of this company's buses is actually less than 264 feet. perform an appropriate hypothesis test. be sure to clearly define your parameter, check your conditions, and list all four steps of the test.

Answer 1

Explanation:

Given that a study found that the average stopping distance of a school bus traveling 50 mph was 264 feet.

Sample taken showed the following results

`n=40\\\bar x =262.3 feet\\Std dev = \sigma= 3 ft`

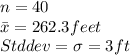
Since population std deviation is known and sample size is large, z test can be used.

`H_0: \bar x=264\\H_a: \bar x <264`

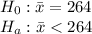
(Left tailed test)

Mean difference =
`264-262.3 = 1.7`

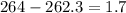
Std error =
`(\sigma)/(√(n) ) \\=(3)/(√(40) ) \\=0.474`

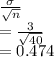
Z = test statistic = mean diff/std error

=
`(1.7)/(0.474) \\=3.584`

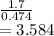
p value = 0.00017

Since p < alpha our 0.05 we reject null hypothesis

There is evidence to show that mean is less than 264 feet

(Assumptions:

Sample are randomly drawn

Sample represents the population