Question

Parking Hoping to lure more shoppers downtown, a city builds a new public parking garage in the central business district. The city plans to pay for the structure through parking fees. Dur-ing a two-month period (44 weekdays), daily fees collected av-eraged $126, with a standard deviation of $15. a) What assumptions must you make in order to use these statistics for inference? b) Write a 90% confidence interval for the mean daily income this parking garage will generate. c) Interpret this confidence interval in context. d) Explain what "90% confidence" means in this context. e) The consultant who advised the city on this project predicted that parking revenues would average $130 per day. Based on your confidence interval, do you think the consultant was correct? Why?

Answer 1

Explanation:

Hello!

a.

Your study variable is X: "daily income of a parking garage"

The parameter to estimate is the population mean (μ) of the daily income of the parking garage. Since the population mean is a parameter of the normal distribution you need your study variable to be normally distributed to study it. If your study variable hasn't the required distribution, since you have a big enough sample, apply the Central Limit Theorem to approximate the sample mean distribution to normal.

So the assumption you need to make is that X[bar]≈N(μ;δ²/n)

b.

The formula for the Confidence Interval is:

X[bar]±
`Z_(1-\alpha /2)`*(S/√n)

I don't have the value of the population standard deviation, so I'll use the approximation with the sample standard deviation.

Sample

n=44

X[bar]= $126

S= $15

`Z_(1-\alpha /2) = Z_(0.90) =1.64`

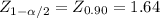
X[bar]±
`Z_(1-\alpha /2)`*(S/√n)

[126±1.64*(15/√44)]

[122.29;129.71]

c.

With a confidence level of 90%, you can expect the interval [122.29;129.71] will contain the true mean of the daily income of the parking garage.

d.

90% of confidence means that if you were to take 100 samples and calculate a confidence interval for the population mean of the daily income of the parking garages, you'd expect 90 of those intervals to contain the true value of the parameter.

e.

If I were to make a hypothesis test to see if the consultant was right, using the complemental level of significance, since the interval doesn't contain the supposed value of $130, I would reject the null hypothesis and conclude that he wasn't right.

H₀: μ = 130

H₁: μ ≠ 130

α: 0.10

[122.29;129.71]

Interval doesn't include 130 ⇒ to Reject the null hypothesis.

I hope this helps!