To develop the problem it is necessary to use the concepts related to density and its definition with respect to mass and volume, as well

Therefore to calculate the volume of woman:
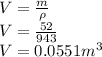
Now, volume of water of Great Salt Lake with the mass of 52 kg,
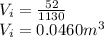
So, percentage of her volume changed will be,
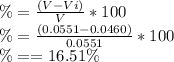
Therefore the percentage of her volume that will be above the waterline of the Great Salt Lake is 16.51%