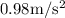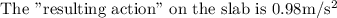Question

A 40 kg slab rests on a frictionless floor. A 10 kg block rests on top of the slab (Fig. 6-58). The coefficient of static friction µstat beltween the block and the slab is 0.70, whereas their kinetic friction coefficient µkin is 0.40. The 10 kg block is pulled by a horizontal force with a magnitude of 100 N.

Answer 1

`\text { The`

Step-by-step explanation:

Normal reaction from 40 kg slab on 10 kg block

M × g = 10 × 9.8 = 98 N

Static frictional force = 98 × 0.7 N

Static frictional force = 68.6 N is less than 100 N applied

10 kg block will slide on 40 kg slab and net force on it

= 100 N - kinetic friction

`=100-(98 * 0.4)\left(\mu_{\text {kinetic }}=0.4\right)`

= 100 - 39.2

= 60.8 N

`10 \mathrm{kg} \text { block will slide on } 40 \mathrm{kg} \text { slab with, } \frac{\mathrm{Net} \text { force }}{\text { mass }}`

`10 \mathrm{kg} \text { block will slide on } 40 \mathrm{kg} \text { slab with }=(60.8)/(10)`

`10 \mathrm{kg} \text { block will slide on } 40 \mathrm{kg} \text { slab with }=6.08 \mathrm{m} / \mathrm{s}^(2)`

`\text { Frictional force on 40 kg slab by 10 kg block, normal reaction * \mu_(kinetic ) }`

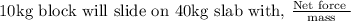
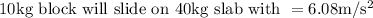
Frictional force on 40 kg slab by 10 kg block = 98 × 0.4

Frictional force on 40 kg slab by 10 kg block = 39.2 N

`40 \mathrm{kg} \text { slab will move with } \frac{\text { frictional force }}{\text { mass }}`

`40 \mathrm{kg} \text { slab will move with }=(39.2)/(40)`

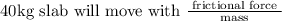
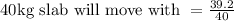
40 kg slab will move with =
`0.98 \mathrm{m} / \mathrm{s}^(2)`

`\text { The`