Answer:
Option B.
Explanation:
If a quadratic equation is defined as
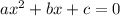 , the by quadratic formula
, the by quadratic formula
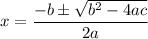
Consider the given equation is
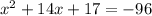
We need to find the value of x.
Add 96 on both sides.
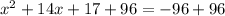
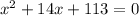
Here, a=1, b=14 and c=113. Using quadratic formula we get
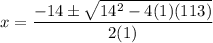
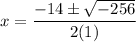
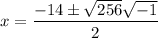
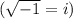
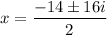
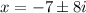
The value of x are x=-7 + 8i and x=-7 - 8i.
Therefore, the correct option is B.