Question

A ship sails 30.50 mi due East and then turns 33.75 north of East. After sailing another 18.53 mi, where is it with reference to the starting point

Answer 1

A ship sails 30.50 mi due East and then turns 33.75 degree north of East. After sailing another 18.53 mi, where is it with reference to the starting point

Answer:

The ship is 18.269 miles distance north of east from starting point

Solution:

Given that ship sails 30.50 miles east

North of east = 18.53 miles

Angle between two sides = 33.75 degree

The figure is attached below

In the figure, A represents starting point

AB = c represents the ship distance with reference to starting point

By using law of cosines,

`c^(2)=a^(2)+b^(2)-2 a b \cos c`

`c^(2)=(30.50)^(2)+(18.53)^(2)-2(30.50)(18.53) \cos 33.75`

`c^(2)=930.259+343.3609-939.835`

`\begin{aligned} c^(2) &=333.7849 \\\\ c &=\pm 18.269 \end{aligned}`

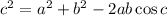
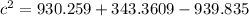
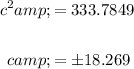
Ignore negative value as we measure distance in positive

c = 18.269

It is 18.269 miles distance north of east from starting point