Question

A long, straight wire carrying a current of 380 A is placed in a uniform magnetic field that has a magnitude of 6.59 × 10-3 T. The wire is perpendicular to the field. Find a point in space where the net magnetic field is zero. Locate this point by specifying its perpendicular distance from the wire.

Answer 1

The point in space where the net magnetic field is zero lies by specifying its perpendicular distance from the wire is 0.01153 m.

Step-by-step explanation:

Given that,

Current = 380 A

Magnetic field
`B=6.59*10^(-3)\ T`

We need to calculate the distance

Using formula of magnetic field

`B = (\mu_(0)I)/(2\pi r)`

`r=(\mu_(0)I)/(2\pi B)`

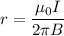
Where, B = magnetic field

I = current

Put the value into the formula

`r=(4\pi*10^(-7)*380)/(6.59*10^(-3)*2\pi)`

`r=0.01153\ m`

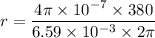
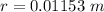
Hence, The point in space where the net magnetic field is zero lies by specifying its perpendicular distance from the wire is 0.01153 m.