Question

What is the justification for the first step in proving the formula for factoring the sum of cubes?

a^3+b^3= (a + b)(a? - ab +62)

= - ab + ab + a²b-ab2 +63

Answer 1

Step-by-step explanation:

The formula isnt correctly written, it should state:

`a^3+b^3 = (a+b)(a^2-ab+b^2)`

You have to start from
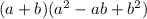`(a+b)(a^2-ab+b^2)` and end in a³+b³. On your first step, you need to use the distributive property.

`(a+b)(a^2-ab+b^2) = a*(a^2-ab+b^2) + b*(a^2-ab+b^2)`

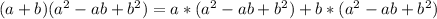
This is equal to

`a*a^2-a*(ab) + a*b^2 + b*a^2-b*(ab) + b*b^2 = a^3 - a^2b + ab^2 +ba^2 -b^2a +b^3`

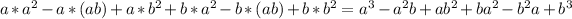
Note that the second term, -a²b, is cancelled by the fourth term, ba², and the third term, ab², is cancelled by the fifht term, -b²a. Therefore, the final result is a³+b³, as we wanted to.