Question

Your friend attempted to factor an expression as shown. Find the error in your friends work. Then factor the expression correctly. Show work please.

2x^2-7x+5

2x^2-5x-2x+5

x(2x-5)+(2x-5)

(x+1)(2x-5)

Answer 1

Third step is incorrect. The correct factored form is (x-1)(2x-5).

Explanation:

The given expression is

`2x^2-7x+5`

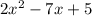
We need to find the factored form of this expression.

Step 1: Given

`2x^2-7x+5`

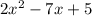
Step 2: Splitting the middle term method, the middle term can be written as (-5x-2x).

`2x^2-5x-2x+5`

`(2x^2-5x)+(-2x+5)`

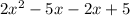
Step 3: Taking out common factors from each parenthesis.

`x(2x-5)-1(2x-5)`

Step 4: Taking out common factors.

`(x-1)(2x-5)`

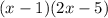
Therefore, the third step is incorrect. The correct factored form is (x-1)(2x-5).