Answer:
The truck will reach there in 250 seconds.
Step-by-step explanation:
The frequency due to doppler effect, when the observer is stationary and the source is moving towards it is
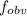 =
=
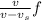
where v= velocity of sound in air
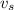 = velocity of source of sound
= velocity of source of sound
f= frequency of sound and
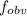 = frequency oberved due to Doppler effect
= frequency oberved due to Doppler effect
 = 460------------------------------------------( 1 )
= 460------------------------------------------( 1 )
The frequency due to doppler effect, when the observer is stationary and the source is moving away from it
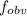 =
=
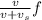
where v= velocity of sound in air
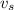 = velocity of source of sound
= velocity of source of sound
f= frequency of sound and
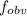 = frequency oberved due to Doppler effect
= frequency oberved due to Doppler effect
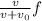 = 410-------------------------------------------( 2 )
= 410-------------------------------------------( 2 )
Dividing ( 1 ) by ( 2 )
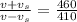
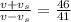
41v + 41
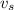 = 46v - 46
= 46v - 46
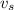
87
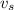 = 5v
= 5v
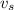 =
=
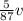
Velocity of Sound (v)= 348 m/s
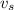 =20 m/s
=20 m/s
Therefore, the truck is moving at 20 m/s.

Distance= 5000 m
Time=
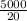
Time= 250 s
Time = 4 min 10 sec