To solve this problem it is necessary to apply the concepts related to Newton's second law and its derived expressions for angular and linear movements.
Our values are given by,
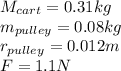
If we carry out summation of Torques on the pulley we will have to,
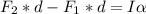
Where,
I = Inertia moment
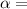 Angular acceleration, which is equal in linear terms to a/r (acceleration and radius)
Angular acceleration, which is equal in linear terms to a/r (acceleration and radius)
The moment of inertia for this object is given as
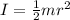
Replacing this equations we have know that
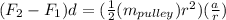
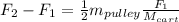
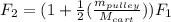
Or
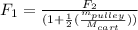
Replacing our values we have that
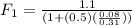
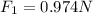
Therefore the tension in the string between the pulley and the cart is 0.974 N