Question

You drop a steel ball bearing, with a radius of 2.40 mm, into a beaker of honey. Note that honey has a viscosity of 6.00 Pa/s and a density of 1360 kg/m3, and steel has a density of 7800 kg/m3. Assume that g = 9.8 m/s2. (a) What is the terminal speed of the ball bearing?

Answer 1

The “terminal speed” of the ball bearing is 5.609 m/s

Step-by-step explanation:

Radius of the steel ball R = 2.40 mm

Viscosity of honey η = 6.0 Pa/s

`\text { Viscosity has Density } \sigma=1360 \mathrm{kg} / \mathrm{m}^(3)`

`\text { Steel has a density } \rho=7800 \mathrm{kg} / \mathrm{m}^(3)`

`\left.\mathrm{g}=9.8 \mathrm{m} / \mathrm{s}^(2) \text { (g is referred to as the acceleration of gravity. Its value is } 9.8 \mathrm{m} / \mathrm{s}^(2) \text { on Earth }\right)`

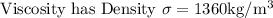
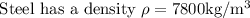
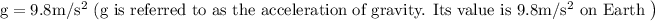
While calculating the terminal speed in liquids where density is high the stokes law is used for viscous force and buoyant force is taken into consideration for effective weight of the object. So the expression for terminal speed (Vt)

`V_(t)=\frac{2 \mathrm{R}^(2)(\rho-\sigma) \mathrm{g}}{9 \eta}`

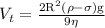
Substitute the given values to find "terminal speed"

`\mathrm{V}_{\mathrm{t}}=(2 * 0.0024^(2)(7800-1360) 9.8)/(9 * 6)`

`\mathrm{V}_{\mathrm{t}}=(0.0048 * 6440 * 9.8)/(54)`

`\mathrm{V}_{\mathrm{t}}=(302.9376)/(54)`

`\mathrm{V}_{\mathrm{t}}=5.609 \mathrm{m} / \mathrm{s}`

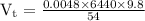
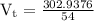
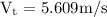
The “terminal speed” of the ball bearing is 5.609 m/s