Answer:
77.
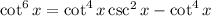 Proved
Proved
78.
![\sec^(4)x \tan^(2) x = \sec^(2)x [\tan^(2)x + \tan^(4)x ]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jjuh6fsc3wn8sohh4dkillcyof4h2uk9sy.png) Proved
Proved
79.
![\cos^(3) x\sin^(2) x = [\sin^(2)x - \sin^(4)x] \cos x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/vbud67snnrrrotrfatu8exixdfsymrk420.png) Proved.
Proved.
80.
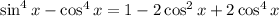 Proved.
Proved.
Explanation:
77. Left hand side
=
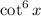
=
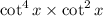
=
![\cot^(4)x [\csc^(2)x - 1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/jfar474d8x854kwjh00ow8k5s0hxffaccu.png)
{Since we know,
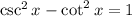 }
}
=
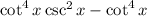
= Right hand side (Proved)
78. Left hand side
=
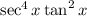
=
![\sec^(2) x [1 + \tan^(2)x] \tan^(2) x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qipzgr9qib3smaltzum6m4rdkdao5nvwc8.png)
{Since
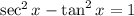 }
}
=
![\sec^(2)x [\tan^(2)x + \tan^(4)x ]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/nv4z53i924v4ocxzz97f7z62at6xhntocd.png)
= Right hand side (Proved)
79. Left hand side
=
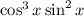
=
![\cos x[1 - \sin^(2) x] \sin^(2) x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ykujx2xhh9eoi9veqhhtfaspq48mjdsg0b.png)
{Since
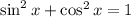 }
}
=
![[\sin^(2)x - \sin^(4)x] \cos x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/q4u70tg10c0h9wic0moh8esyejvopi9x3k.png)
= Right hand side
80. Left hand side
=

=
![[\sin^(2)x + \cos^(2)x]^(2) - 2\sin^(2) x \cos^(2)x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4mp2j444xks9qmvqdnysjz691urgy5ufmj.png)
{Since
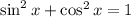 }
}
=
![1 - 2\cos^(2) x[1 - \cos^(2)x ]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/vb0zd23c4cq7v7djv2fvyhiw8nbtifav2x.png)
=
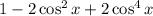
= Right hand side. (Proved)