Answer:
f(g(x)) = g(f(x)) = x and f and g are the inverses of each other.
Explanation:
Here, the given functions are:
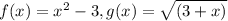
To Show: f (g(x)) = g (f (x))
(1) f (g(x))
Here, by the composite function:
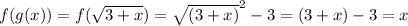
⇒ f (g(x)) = x
(2) g (f(x))
Here, by the composite function:
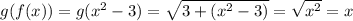
⇒ g (f(x)) = x
Hence, f(g(x)) = g(f(x)) = x
⇒ f and g are the inverses of each other.