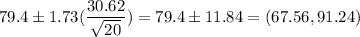Question

How much does a sleeping bag cost? Let's say you want a sleeping bag that should keep you warm in temperatures from 20°F to 45°F. A random sample of prices ($) for sleeping bags in this temperature range is given below. Assume that the population of x values has an approximately normal distribution. 35 85 105 40 100 50 30 23 100 110 105 95 105 60 110 120 95 90 60 70 (a) Use a calculator with mean and sample standard deviation keys to find the sample mean price x and sample standard deviation s. (Round your answers to two decimal places.) x = $ 79.4 Correct: Your answer is correct. s = $ 30.62 Correct: Your answer is correct. (b) Using the given data as representative of the population of prices of all summer sleeping bags, find a 90% confidence interval for the mean price μ of all summer sleeping bags. (Round your answers to two decimal places.)

Answer 1

a) Sample Mean = 79.4

Sample standard deviation = 30.62

b) 90% Confidence interval: (67.56 ,91.24)

Explanation:

We are given the following in the question:

Prices for sleeping bags has an approximately normal distribution.

We are given the following sample:

35, 85, 105, 40, 100, 50, 30, 23, 100, 110, 105, 95, 105, 60, 110, 120, 95, 90, 60, 70

a)

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(1588)/(20) = 79.4`

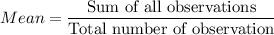
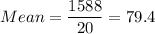
Sum of squares of differences = 1971.36 + 31.36 + 655.36 + 1552.36 + 424.36 + 864.36 + 2440.36 + 3180.96 + 424.36 + 936.36 + 655.36 + 243.36 + 655.36 + 376.36 + 936.36 + 1648.36 + 243.36 + 112.36 + 376.36 + 88.36 = 17816.8

`S.D = \sqrt{\displaystyle(17816.8)/(19)} = 30.62`

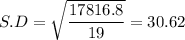
b) 90% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

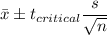
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 19 and}~\alpha_(0.10) = \pm 1.7291`

`79.4 \pm 1.73(\displaystyle( 30.62)/(√(20)) ) = 79.4 \pm 11.84 = (67.56 ,91.24)`