Answer:
Volume is
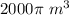
Solution:
As per the question:
Diameter, d = 40 m
Radius, r = 20 m
Now,
From north to south, we consider this vertical distance as 'y' and height, h varies linearly as a function of y:
iff
h(y) = cy + d
Then
when y = 1 m
h(- 20) = 1 m
1 = c.(- 20) + d = - 20c + d (1)
when y = 9 m
h(20) = 9 m
9 = c.20 + d = 20c + d (2)
Adding eqn (1) and (2)
d = 5 m
Using d = 5 in eqn (2), we get:
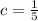
Therefore,
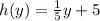
Now, the Volume of the pool is given by:
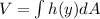
where
A =
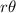
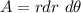
Thus
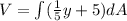

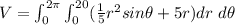
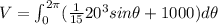
![V = [- 533.33cos\theta + 1000\theta]_(0)^(2\pi)](https://img.qammunity.org/2020/formulas/mathematics/high-school/xl10fr217ypp88aromihm43ue3o25v12xp.png)
