Question

The angle of depression from the top of one building to the foot of a building across the street is 53°. The angle of depression to the top of the same building is 19°. The two buildings are 80 feet apart. What is the height of the shorter building?

Answer 1

78.64 feet

Explanation:

Refer the attached figure

Height of the tall building = AC

The angle of depression from the top of one building to the foot of a building across the street is 53°. i.e.∠ADC = 53°

The angle of depression to the top of the same building is 19°.i.e.∠AEB = 19°

Height of small building = ED

The two buildings are 80 feet apart i.e. CD =BE= 80 feet

In ΔABC

`Tan \theta = (Perpendicular)/(Base)`

`Tan 53^(\circ)= (AC)/(CD)`

`Tan 53^(\circ)= (AC)/(80)`

`1.327 * 80= AC`

`106.16= AC`

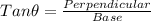
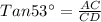
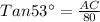
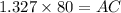
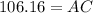
In ΔABE

`Tan \theta = (Perpendicular)/(Base)`

`Tan 19^(\circ)= (AB)/(BE)`

`Tan 19^(\circ)= (AB)/(80)`

`0.344 * 80=AB`

`27.52= AB`

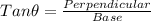
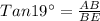
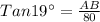
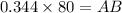
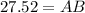
AC - AB = BC

106.16-27.52=BC

78.64=BC

So, BC = ED = 78.64 feet

Hence the height of the shorter building is 78.64 feet