Question

A normally distributed population has a mean of 475 and a standard deviation of 60.

a. Determine the probability that a random sample of size 16 selected from this population will have a sample mean less than 435.
b. Determine the probability that a random sample of size 25 selected from the population will have a sample mean greater than or equal to 501.

Answer 1

Answer: a. 0.0038 b. 0.0151

Explanation:

Given : A normally distributed population has a mean of 475 and a standard deviation of 60.

i.e.
`\mu=475`
`\sigma=60`

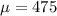
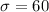
Let
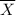`\overline{X}` be the sample mean.

Formula :
`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

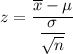
a. For sample n= 16

Then, the probability that a random sample of size 16 selected from this population will have a sample mean less than 435. will be :-

`P(\overline{x}<435)=P(\frac{\overline{x}-\mu}{(\sigma)/(√(n))}<(435-475)/((60)/(√(16))))\\\\\approx P(z<-2.67)\\\\=1-P(z<2.67)\ \ [\because\ P(Z<-z)=1-P(Z<z)]\\\\=1-0.9962=0.0038\ \ \ [ \text{Using z-value table}]`

∴ The probability that a random sample of size 16 selected from this population will have a sample mean less than 435 = 0.0038

b. For sample n= 25

Then, the probability that a random sample of size 16 selected from this population will have a sample mean less than 435. will be :-

`P(\overline{x}\geq501)=P(\frac{\overline{x}-\mu}{(\sigma)/(√(n))}\geq(501-475)/((60)/(√(25))))\\\\\approx P(z\geq2.167)\\\\=1-P(z<2.167)\ \ [\because\ P(Z\geq z)=1-P(Z<z)]\\\\=1-0.9849=0.0151\ \ \ [ \text{Using z-value table}]`

∴ The probability that a random sample of size 25 selected from the population will have a sample mean greater than or equal to 501 = 0.0418