Question

Can someone please help me? Thanks

Answer 1

693 sq. m.

Explanation:

The figure consists of a triangular prism (Bottom Part) and a Triangular Pyramid (Top Part). We will find the volume of each and add it up to get volume of total figure.

1. Volume of Triangular Prism = Area of Triangular Base * Height

Area of Triangular Base = (1/2)*base*height

Given that the triangle is a right triangle, we find the unknown side by using Pythagorean Theorem, which tells us:

Leg^2 + Another Leg^2 = Hypotenuse^2

8.8^2 + Another Leg^2 = 13.7^2

77.44+ Another Leg^2 = 187.69

Another Leg (unknown side, or the base of the triangle) = Sqrt(187.69-77.44) = 10.5 (this is base of triangle)

So, we have:

Area of Triangular Base =
`(1)/(2)*10.5*8.8=46.2`

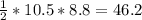
Thus,

Volume of Triangular Prism = 46.2 * 10(given) = 462 sq.m.

2. Volume of Triangular Pyramid = (1/3) * area of triangular base * height

Here, area of triangular pyramid is 46.2 (already found)

the height of the pyramid is 25 - 10 = 15

SO, we have:

Volume of Triangular Pyramid =
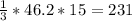`(1)/(3)*46.2*15=231` sq. m.

Now we sum them up and get total volume of the figure:

Total Volume of Figure = 462+ 231 = 693 sq. m.