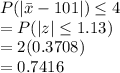Answer:
101, 3, 0.025, 0.7416
Explanation:
Given that a random sample of n = 16 observations is selected from a population that is normally distributed with mean equal to 101 and standard deviation equal to 12.
As per central limit theorem we have
a) Mean of sample mean =
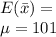
Std deviation of sample mean =

Mean = 101
Std dev =3.00
b)

c) the probability that the sample mean deviates from the population mean μ = 101 by no more than 4.
=