Question

The producer of a certain medicine claims that its bottling equipment is very accurate and that the standard deviation of all its filled bottles is 0.1 ounce or less. A sample of 20 bottles showed a standard deviation of .11. The test statistic to test the claim is _____.

Answer 1

Answer: The test statistic to test the claim is
`\chi^2=22.99`.

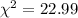Explanation:

Let
`\sigma` be the standard deviation of filled bottles.

As per given , we have

`H_0:\sigma=0.1\\\\ H_1:\sigma\\eq0.1`

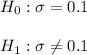
To fins test statistic , we use Chi -square test for population standard deviation:

`\chi^2=((n-1)s^2)/(\sigma^2)`

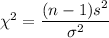
, where n= sample size .

s= sample standard deviation.

We are given that , n= 20 and s= 0.11

Then,
`\chi^2=((20-1)(0.11)^2)/((0.1)^2)`

`\chi^2=((19)(0.0121))/(0.01)=22.99`

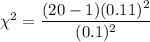
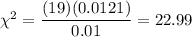
Hence, the test statistic to test the claim is
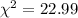`\chi^2=22.99`.