Answer: There is sufficient evidence to support the claim that the bags are under-filled.
Explanation:
Since we have given that
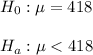
Sample mean = 411
Standard deviation = 20
n = 9
So, the test statistic value is given by
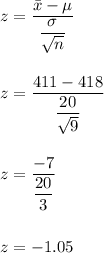
At 0.025 level of significance,
critical value z = -2.306
since -2.306<-1.05
so, we will reject the null hypothesis.
Yes, there is sufficient evidence to support the claim that the bags are underfilled.