Answer:
0.2 tesla
Step-by-step explanation:
Number of turn, N = 101
Area, A = 5.61 x 10^-4 m^2
angle between the magnetic moment and magnetic field, θ = 48.9°
Torque, τ = 2.75 x 10^-5 Nm
Current, i = 0.00339 A
Let the magnetic field strength is B.
The formula for the torque is given by
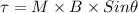
where, M is the magnetic moment
M = N x i x A = 101 x 0.00339 x 5.61 x 10^-4 = 1.92 x 10^-4 Am^2
By substitute the values
2.75 x 10^-5 = 1.92 x 10^-4 x B x Sin 48.9°
B = 0.189 Tesla
B = 0.2 Tesla