Question

The brightness of a picture tube can be evaluated by measuring the amount of current required to achieve a particular brightness level. A sample of 10 tubes results in ¯x = 317.2 and s = 15.7 measured in microamps. (a) Find a 99% CI on mean current required.

Answer 1

The 99% confidence interval for the mean would be (301.064;333.336) mA

Explanation:

1) Notation and some definitions

n=10 sample selected

`\bar x=317.2mA` sample mean for the sample tubes selected

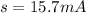`s=15.7mA` sample deviation for the sample selected

Confidence = 99% or 0.99

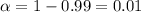`\alpha=1-0.99=0.01` significance level

A confidence interval for the mean is used to "places boundaries around an estimated
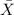`\bar X` so that the true population mean
`\mu` would be expected to lie within those boundaries with a confidence specified. If the uncertainty is large, then the interval between the boundaries must be wide; if the uncertainty is small, then the interval can be narrow"

2) Formula to use

For this case the sample size is <30 and the population standard deviation
`\sigma` is not known, so for this case we can use the t distributon to calculate the critical value. The first step would be calculate alpha

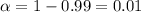`\alpha=1-0.99=0.01` and
`\alpha/2=0.005`, then we can calculate the degrees of freedom given by:

`df=n-1=10-1=9`

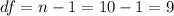
Now we can calculate the critical value
`t_(\alpha/2)=3.25`

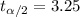
And then we can calculate the confidence interval with the following formula

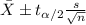`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

3) Calculate the interval

Using the formula (1) and replacing the values that we got we have:

`317.2 - 3.25(15.7)/(√(10))=301.064`

`317.2 + 3.25(15.7)/(√(10))=333.336`

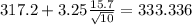
So then the 99% confidence interval for the mean would be (301.064;333.336)mA

Interpretation: A point estimate for the true mean of brightness level for the tubes in the population is 317.2mA, and we are 99% confident that the true mean is between 301.064 mA and 333.336 mA.