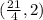Question

Find the coordinates of point B on AC such that Ab, is 1/4 of AC.
​

Answer 1

5,2 is correct answer

Explanation:

Answer 2

The coordinates of point B is
`((21)/(4) , 2 )`

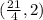
Explanation:

Given:

Let,

`B \equiv (x,y)\\A \equiv (x1,y1) \equiv (7,4)\\C \equiv (x2,y2) \equiv (0,-4)`

`(AB)/(AC) =(1)/(4)`

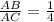
First we need to find
`(AB)/(BC)`

`\therefore (AB)/(AC) = (1)/(4)\\\therefore (AC)/(AB) = (4)/(1)\ Invertendo\\\therefore (AC-AB)/(AB) = (4-1)/(1)\ Dividendo\\ \therefore (BC)/(AB) = (3)/(1)\\ \therefore (AB)/(BC) = (1)/(3)\ Invertendo\\\therefore (AB)/(BC) = (1)/(3) = (m)/(n)\ say`

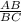
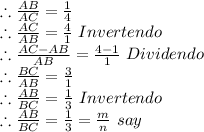
Now point B divide segment AC internally in the ratio m : n i.e 1/3.

So, by internal division formula, the X coordinate and the Y coordinate of point B are as follow

`x =(mx2+nx1)/(m+n)\ and\ y = (my2+ny1)/(m+n)\\x =(1* 0 + 3* 7)/(1+3)\ and\ y =(1* -4 + 3* 4)/(1+3)\\x =(21)/(4)\ and\ y =(8)/(4)\\x =(21)/(4)\ and\ y = 2`

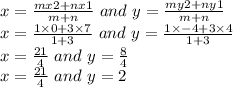
Therefore,The coordinates of point B is
`((21)/(4) , 2 )`