Answer:
The maximal margin of error associated with a 95% confidence interval for the true population mean is 2.238.
Explanation:
We have given,
The sample size n=42
The sample mean
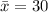
The population standard deviation
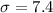
Let
 be the level of significance = 0.05
be the level of significance = 0.05
Using the z-distribution table,
The critical value at 5% level of significance and two tailed z-distribution is
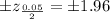
The value of margin of error is
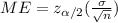
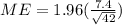
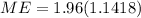
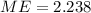
The maximal margin of error associated with a 95% confidence interval for the true population mean is 2.238.