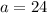Since the multiplicative inverse of a fraction p/q is the fraction that swaps its numerator and denominator, i.e. q/p, we have that the inverse of 2/3 is 3/2.
So, if we multiply both sides of the equation by 3/2, we have
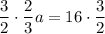
3/2 and 2/3 are multiplicative inverse of each other, and by definition this means that they give 1 when multiplied:

On the right hand side, we have
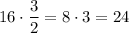
And so the solution is