Answer:
The positive real number is 26
Explanation:
Let
x ----> the number
we know that
The algebraic expression that represent this problem is
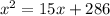
so
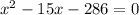
The formula to solve a quadratic equation of the form

is equal to

in this problem we have
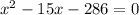
so
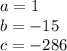
substitute in the formula
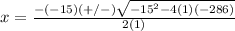
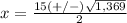
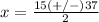
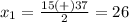
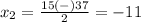 ---> the solution cannot be negative
---> the solution cannot be negative
therefore
The positive real number is 26