Question

A cylindrical can is to hold 20
`\pi` cubic meters. the material for the top and bottom costs $10 per square meter, and material for the side costs $8 per square meter. fond the radius r and the height h of the most economical can i.e. such that the cost is minimal

Answer 1

The cost of the can is minimal when r=2 m and h=5 m

Explanation:

This is an optimization problem which will be solved by the use of derivatives

We must find an expression for the total cost of the cylindrical can and then find its dimensions to make the cost minimal

Let's picture a cylinder of radius r and height h. Its volume is computed as

`V=\pi r^2h`

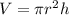
To make the lids we need two circle-shaped pieces of a material which costs $10 per square meter

The area of each lid is

`A_l=\pi r^2`

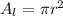
The cost of both lids will be

`C_l=(2)(10)(\pi r^2)=20\pi r^2`

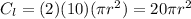
The lateral side of the cylinder can be constructed with a rectangle of material which costs $8 per square meter

The rectangle has a height of h and a width equal to the length of the circumference

`A_s=2\pi rh`

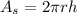
The cost of the side of the cylinder will be

`C_s=16\pi rh`

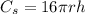
The total cost of the can is

`C=20\pi r^2+16\pi rh`

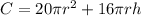
We know the volume of the can is
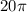`20\pi` cubic meters

`V=\pi r^2h=20\pi`

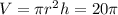
Isolating h we have

`h=(20)/(r^2)`

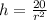
Using this value into the total cost

`C=20\pi r^2+16\pi r((20)/(r^2))`

`C=20\pi r^2+(320\pi)/(r)`

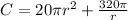
Differentiating with respect to r

`C'=40\pi r-(320\pi)/(r^2)`

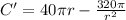
To find the critical point, we must set C'=0

`40\pi r-(320\pi)/(r^2)=0`

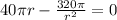
Operating

`40\pi r^3-320\pi=0`

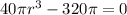
Solving for r

`r=\sqrt[3]{(320\pi)/(40\pi)}=\sqrt[3]{8}`

r=2

And since

`h=(20)/(r^2)=(20)/(2^2)`

h=5

Differentiating again we find

`C''=40\pi +(640\pi)/(r^3)`

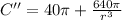
Which is always positive for r positive. It makes the critical point found a minimum

The cost of the can is minimal when r=2 m and h=5 m