Answer:
Part a)
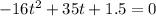
Part b)
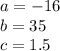
Part c) The soccer ball will take 2.23 seconds to reach the ground
Explanation:
we have
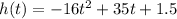
where
t is the time the ball has been in the air, in seconds
h(t) is the height, in feet, of the soccer ball
Part a) Write an equation that could be used to determine the time the ball traveled before it hit the ground
we know that
When the ball hit the ground, the value of h(t) is equal to zero
so
For h(t)=0
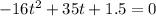
This equation can be used to determine the time the ball traveled before it hit the ground
Part b) Determine the values of a, b, and c
we know that
The formula to solve a quadratic equation of the form

is equal to

in this problem we have
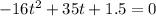
so
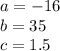
Part c) How long will it take for the soccer ball to reach the ground after it was kicked?
Solve the quadratic equation by the formula

we have
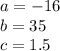
substitute the values
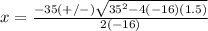
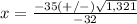
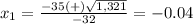 ---> cannot be a solution (is negative)
---> cannot be a solution (is negative)
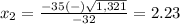
therefore
The soccer ball will take 2.23 seconds to reach the ground