Answer:
3.07 seconds is the half-life of the isotope.
Step-by-step explanation:
Initial mass of an isotope = x
Time taken by the sample, t = 8.40 s
Mass of an isotope decayed= 85.0%
Final mass of an isotope left=(100%-85%)of x= 15.0% of x = 0.15x
Half life of an isotope =
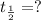
Formula used :
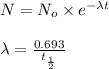
where,
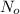 = initial mass of isotope
= initial mass of isotope
N = mass of the parent isotope left after the time, (t)
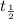 = half life of the isotope
= half life of the isotope
 = rate constant
= rate constant
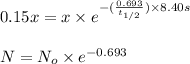
Now put all the given values in this formula, we get
![t_{1/2]=3.07 s](https://img.qammunity.org/2020/formulas/chemistry/middle-school/dz4uehy1vlgiyd6wy2t9br6168n8p2vngb.png)
3.07 seconds is the half-life of the isotope.