Question

A 2.8-carat diamond is grown under a high pressure of 58 × 10 9 N / m 2 .

(a) By how much does the volume of a spherical 2.8-carat diamond expand once it is removed from the chamber and exposed to atmospheric pressure?
(b) What is the increase in the diamond’s radius? One carat is 0.200 g, and you can use 3.52 g/cm3 for the density of diamond, and 4.43 × 10 11 N / m 2 for the bulk modulus of diamond.

Answer 1

a) ΔV = 2,118 10⁻⁸ m³ b) ΔR= 0.0143 cm

Step-by-step explanation:

a) For this part we use the concept of density

ρ = m / V

As we are told that 1 carat is 0.2g we can make a rule of proportions (three) to find the weight of 2.8 carats

m = 2.8 Qt (0.2 g / 1 Qt) = 0.56 g = 0.56 10-3 kg

V = m / ρ

V = 0.56 / 3.52

V = 0.159 cm3

We use the relation of the bulk module

B = P / (Δv/V)

ΔV = V P / B

ΔV = 0.159 10⁻⁶ 58 10⁹ /4.43 10¹¹

ΔV = 2,118 10⁻⁸ m³

b) indicates that we approximate the diamond to a sphere

V = 4/3 π R³

For this part let's look for the initial radius

R₀ = ∛ ¾ V /π

R₀ = ∛ (¾ 0.159 /π)

R₀ = 0.3361 cm

Now we look for the final volume and with this the final radius

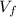`V_(f)` = V + ΔV

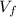`V_(f)` = 0.159 + 2.118 10⁻²

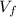`V_(f)` = 0.18018 cm3

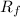`R_(f)` = ∛ (¾ 0.18018 /π)

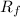`R_(f)` = 0.3504 cm

The radius increment is

ΔR =
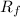`R_(f)` - R₀

ΔR = 0.3504 - 0.3361

ΔR= 0.0143 cm